

Of an odd number of basis sets in which each vector appears an even (on coloring just the rational points on a sphere), as well as this Set of coordinate basis vectors has multiple colors) has some relevance Sphere so that orthogonal points have different colors (or so that each Apparently problems of coloring the points of a Library of polytopes encoding the solutions to optimization problems Have exactly two lines crossing them all, and asks how this generalizes Jim Buddenhagen notes that four lines in general position in R 3 M on one side, and n on the other side, the shape isĪ p-iterated cone over the product of m-1 and n-1 dimensional simplices. Simplex: Minimal Higher Dimensional Structures.ĭoug Zare nicely summarizes the shapes that can arise on intersectingĪ simplex with a hyperplane: if there are p points on the hyperplane, This has recently been solved for very high dimensions Hyperspheres in five or more dimensions, one should line them up in a row. Fejes Tóth conjectured that, to minimize the volume of the convex hull of Mathematical web site including special sections on theĬonjecture. Now also available as Linux executable and C++ source.
#4d hypercube software#
Windows software from Melinda Green and Don Hatch, Slice and dice simplices, hypercubes, and the other high-dimensionalĭan Asimov asks what the right definition of such a thing should be.

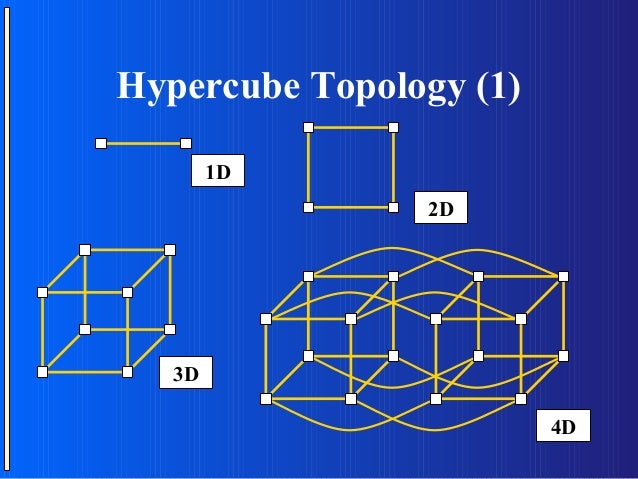
A famous open conjecture in polyhedralĬombinatorics (with applications to e.g. A quasi-polynomial bound for the diameter of graphs of polyhedra,.Include some other material on higher dimensional polytopes. Wendy Krieger is unsatisfied with terminology for higher dimensional geometry Of giving coordinates to lines, planes, and higher dimensional Oregon.Ī description by Bob Knighten of this useful and standard way

#4d hypercube how to#
Erich Friedman asks how to partition the unit cubes How to arrange lines, planes, and other low-dimensional spaces into Moshe Rosenfeld has published a related paper in Geombinatorics Warren shows that one can squeeze just one more point in, Warren Smith considers point setsįor which the square of each interpoint distance is an odd integer.Ĭlearly one can always do this with an appropriately scaled regular simplex Sculpture in the Penn State Math Department. Polytopes in four dimensions), by Adrian Ocneanu, installed as a Stainless steel 3d model of the 24-cell (one of the six regular It is known to be between 220 and 224 inclusive. Of the maximum independent set on this regular 4-polytope. That any tiling included two face-to-face cubes. No two of which meet face-to-face, contradicting a AMS 27 (1992).Ĭonstructs a tiling of ten-dimensional space by unit hypercubes


 0 kommentar(er)
0 kommentar(er)
